つくってまなぼう 自動微分 (Automatic Differentiation)
導入
機械学習で予測問題(Regression や Classification)を解くステップは、大きく以下のように分解することができます:
- 予測器となる関数をモデル化(CNN、RNNなど)
- 予測結果を評価するための損失関数を定義(自乗誤差、Cross Entropyなど)
- 勾配法によって損失を最小化
- 勾配を計算(backpropagation)
- パラメータを更新(SGD、Adamなど)
Neural Network などの機械学習でよく用いられるモデルは、シンプルな関数を合成や四則演算などで組み合わせた巨大な計算グラフの形をしています。そんな関数の勾配を効率的に計算するためには工夫が必要で、標準的な方法として知られているのが backpropagation です。
実は、この backpropagation は Automatic Differentiation (AD) と呼ばれるアルゴリズムの特殊ケースに当たり、機械学習が脚光を浴びるより前から提案されていました。
ADの中心的なアイデア
微分の連鎖律
Neural Network は全体として見ると非常に複雑な関数ですが、パーツ単位で見れば線形関数やsigmoid関数など導関数が既知のシンプルな関数で構成されています。
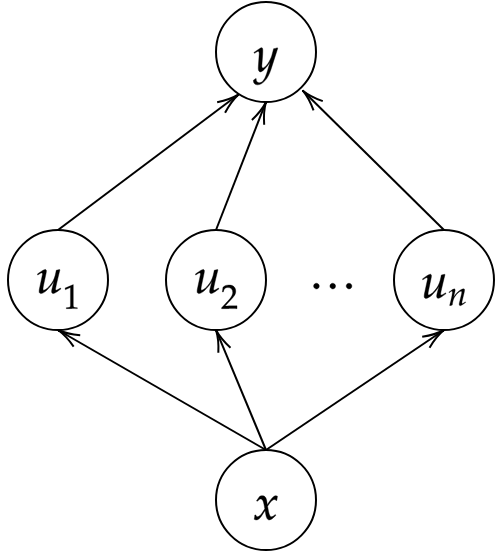
そこで役に立つのが、合成関数に対する微分の連鎖律です。例えば、上図のように変数 が変数
だけに依存し、更に
が
に依存している場合、連鎖律は次式のように表されます:
$$ \dfrac{\partial y}{\partial x} = \dfrac{\partial y}{\partial u_1}\dfrac{\partial u_1}{\partial x} + \dfrac{\partial y}{\partial u_2}\dfrac{\partial u_2}{\partial x} + \cdots + \dfrac{\partial y}{\partial u_n}\dfrac{\partial u_n}{\partial x} $$
この関係を利用すると、式 の微分という問題を、より細かな部分式
および
の微分という問題に分解することができます。更に、各部分式について再帰的に連鎖律を適用することで、最終的には導関数が既知の関数まで到達します。
この素朴なアイデアに基づいて、機械的に微分を計算する Python スクリプトを実装します。大まかな仕様は:
- 計算式を表現するためのデータ型として
Exprクラスを定義 argsプロパティで、引数の計算式を表すExprオブジェクトを参照ExprオブジェクトyとSymbolオブジェクトxに対して、y.diff(x)は関数の導関数を表す
Exprオブジェクトを返す
def dot(xs, ys): return Plus(*[Product(x, y) for x, y in zip(xs, ys)]) class Expr: def diff(self, symbol): diffs = [arg.diff(symbol) for arg in self.args] grad = self.grad() return dot(diffs, grad) class Symbol(Expr): def __init__(self, symbol): self.symbol = symbol def diff(self, symbol): if self == symbol: return Constant(1) else: return Constant(0) class Constant(Expr): def __init__(self, value): self.value = value def diff(self, symbol): return Constant(0) class Plus(Expr): def __init__(self, *args): self.args = args def grad(self): return [Constant(1)] * len(self.args) class Product(Expr): def __init__(self, arg0, arg1): self.args = [arg0, arg1] def grad(self): arg0, arg1 = self.args return [arg1, arg0]
特に5~8行目の関数 diff が、前述の連鎖律を用いて再帰的に定義されている部分です。コード中の変数名と式中の記号に対応を付けると:
Exprオブジェクト ↔symbol↔args↔diffs↔grad↔
上記のコードが正しく動くことを確認するために、 Expr オブジェクトを文字列に変換する方法を定義します。
Symbol.__str__ = lambda self: str(self.symbol) Constant.__str__ = lambda self: str(self.value) Plus.__str__ = lambda self: ' + '.join(['(' + str(arg) + ')' for arg in self.args]) Product.__str__ = lambda self: ' * '.join([str(arg) for arg in self.args])
例として を微分してみると以下のような結果になります。冗長な見た目ではありますが、
と等価な式になっていることがわかります。
x = Symbol('x') y = Plus(x, Product(x, x)) dy = y.diff(x) str(dy) # '(1 * 1) + ((1 * x) + (1 * x) * 1)'
動的計画法
前述の素朴な実装はADと呼べる代物ではなく、分割統治法に共通して存在する欠陥を抱えています。その欠陥とはつまり、同一の部分式に対する微分計算を無駄に多数回繰り返してしまうことです。

上図のような計算式 を変数
について微分する場合を考えましょう。前述の
diff メソッドは、式 y を始点として引数を再帰的に(矢印を逆方向に)辿っていきます。このとき、 上図のグラフはツリーではなく Directed Acyclic Graph (DAG) になっているので、 から
に至る経路が複数(
個)存在します。従って、関数
の微分を計
回計算することになりますが、何度計算しても同じ結果が返されるだけなので非常に効率が悪いです。
そこで、次のようにメモ化を用いて実装することで冗長な計算を省くことができます。
- ある部分式について初めて
diffが呼び出されたら普通に微分を計算 - 計算結果をメモリに保存
- 再び同じ部分式について
diffが呼び出されたら保存された結果を再利用
def memoize(f): memo = {} def memoized(*args): if args not in memo: memo[args] = f(*args) return memo[args] return memoized class Expr: @memoize # デコレーターを追加 def diff(self, symbol): # 前述の実装と同じ
評価順序
Forward-mode (bottom-up) AD
前述の実装では、 からスタートして、中間変数
を入力
で微分した値
を徐々に求めていきます。この方法は、元の計算グラフで中間変数の値を計算していくのと同じ順序で微分を計算していくため、 forward-mode AD と呼ばれています。

forward-mode AD を使うと、「各出力 をある1つの入力
で微分した値
」を1度の走査で求めることができます。従って、関数の入力より出力の方が個数が多い場合には、 forward-mode AD が計算量的に有利です。
Reverse-mode (top-down) AD
一方 reverse-mode AD では、 からスタートして、出力
を中間変数
で微分した値
を徐々に求めていきます。

reverse-mode AD を使うと、「ある1つの出力 を各入力
で微分した値
」を1度の走査で求めることができます。従って、関数の出力より入力の方が個数が多い場合には、 reverse-mode AD が計算量的に有利です。特に機械学習の問題では、出力が1つだけの関数の勾配を計算することが多いため reverse-mode AD (backpropagation) が重宝されます。
つづく
次の記事で書く予定の内容:
- reverse-mode AD のPython実装
- ADでよく使われる中間表現( Wengert list など)
- operator overloading
参考文献
- Automatic differentiation in machine learning: a survey
- 初めてADを学ぶのに適した survey 論文
- 記号微分や有限差分近似とADの違いを最初に明確にしている。
- forward-mode, reverse-mode の仕組みとメリットについて説明している。
- Wengert list の例を示している。
- dual number を使った forward-mode AD の実装を説明している。
- ADの歴史や応用例を紹介している。
- 5節で実装の詳細を説明しているが、式や図が無いため初学者には読みづらい。
- Automatic differentiation in ML: Where we are and where we should be going
- Don't Unroll Adjoint: Differentiating SSA-Form Programs
- MikeInnes/diff-zoo: Differentiation for Hackers